PUEDES LEER ESTA MISMA ENTRADA CON ALGUNOS AÑADIDOS Y LIGERAS CORRECCIONES UTILIZANDO ESTE ENLACE (Las fórmulas se ven mejor y las que aquí no se ven, allí sí)
https://parafernaliasviendolasformulas.blogspot.com/2023/12/conjetura-de-collatz-y-constante-de.html
Mucha gente ajena al mundillo de las matemáticas, incluyendo al 90% del alumnado de Secundaria, cree que las matemáticas están ya hechas, que son conocimientos adquiridos de una vez por todas y se sorprenden si se les dice que hay cuestiones abiertas, afirmaciones de las que no se sabe si son verdaderas o falsas.
En esta entrada, además de informar sobre la conjetura de Collatz y la constante de Krapekar, quisiera mostrar que las matemáticas son algo vivo y en construcción y no (sólo) un conjunto de verdades eternas.
Y esto quisiera mostrarlo a través de la distinción más técnica entre "teorema" y "conjetura"
Todo eso con el estilo de este blog de comentar poco y poner enlaces a documentos sobre el tema en cuestión
Un hecho curioso que ilustra la idea de que "no todo está demostrado en matemáticas", es decir que hay cuestiones que todavía no se conocen (exactamente igual que en todas las ciencias) es el siguiente:
¿Hay infinitos números primos en la sucesión de Fibonacci?
https://twitter.com/edusadeci/status/876053730076000256
Sin embargo nos centraremos en las dos cuestiones que mencionamos en el título, comenzando por la conjetura de Collatz. Ello no será obstáculo para tratar "de pasada" otros asuntos mateemáticos.En lo que sigue hay muchos enlaces a materiales escritos y multimedia sobre la conjetura de Collatz, pero voy a empezar por una introducción sencilla, amena y simpática sobre todos los aspectos de la conjetura.
http://www.bbc.com/mundo/noticias-36651490
Quizá éste de arriba sea el documento divulgativo de mayor calidad.
No obstante, ahí van bastantes otros.
Creo que es bueno recurrir a pluralidad de fuentes para informarse sobre cualquier tema.
Empezamos:
Vamos a ver un vídeo que explica sencillamente la conjetura de Collatz
http://www.math2me.com/playlist/curiosidades/siempre-se-llega-a-1-problema-de-collatz
Ahora, atendemos a las explicaciones de un blog
https://www.blogger.com/comment.g?blogID=3219117272340648003&postID=935806891704841038&page=1&token=1457800122525
Continuamos con las reflexiones del comienzo de esta entrada
De hecho, cuando los matemáticos enuncian una afirmación, pero aún no saben si es verdadera o falsa, dicen que han enunciado una conjetura.
Normalmente, existen motivos para sospechar que lo que se enuncia es cierto, pero aún no se dispone de demostración.
Existen muchas de estas cuestiones abiertas o conjeturas.
Lamentablemente para entender lo que dicen esas conjeturas, en la mayor parte de los casos hay que tener grandes conocimientos matemáticos, mucho más allá de lo que se aprende en la enseñanza secundaria o incluso en los primeros cursos universitarios.
Entre las excepciones, es decir, entre las conjeturas cuyo enunciado se comprende fácilmente, hubo una muy famosa conocida como "último teorema de Fermat" que dice:
Este enunciado lo propuso Fermat en 1637 y fué demostrado por Wiles en 1995.
El enunciado era muy fácil de entender, pero la demostración resultó ser muy difícil, y por eso se mantuvo como conjetura durante más de 350 años, hasta que se demostró y pasó a ser TEOREMA.
Aquí tienes información sobre esta conjetura que ya pasó a ser teorema:
http://www.youtube.com/watch?v=BAfPRMgSTfc
http://www.youtube.com/watch?feature=endscreen&v=xisFprlQvC8&NR=1
Los demás vídeos son fáciles de encontrar a partir de estos, hasta 5
Otros documentos:
http://es.wikipedia.org/wiki/%C3%9Altimo_teorema_de_Fermat
http://gaussianos.com/el-ultimo-teorema-de-fermat/
http://buenlibro.blogspot.com.es/2007/09/el-ltimo-teorema-de-fermat.html
http://enciclopedia.us.es/index.php/%C3%9Altimo_teorema_de_Fermat
http://www.portalplanetasedna.com.ar/fermat.htm
http://www.ciencia.cl/CienciaAlDia/volumen2/numero1/articulos/articulo1.html
Podemos decir:
CONJETURA es una afirmación de la que se sospecha que puede ser cierta, pero cuya veracidad aún no está demostrada
TEOREMA es una afirmación de la que existe demostración válida y por tanto de la que se puede asegurar que es cierta.
Por tanto los matemáicos enuncian conjeturas e intentan convertirlas en teoremas
Otro ejemplo de conjetura que tardó casi 100 años en convertirse en teorema, es decir en ser demostrada es la conjetura de Poincaré, propuesta por este matemático en 1904.
Ésta es de las difíciles de entender (y aún más difícil de demostrar)
Coloco aquí lo que dice la Wikipedia de ella:
En matemáticas, y más precisamente en topología, la conjetura de Poincaré (también llamada hipótesis de Poincaré) es un resultado sobre la esfera tridimensional (la 3-esfera); la hipótesis dejó de ser una conjetura para convertirse en un teorema tras su comprobación en 2003 por el matemático Grigori Perelman. El teorema sostiene que la esfera tridimensional, también llamada 3-esfera o hiperesfera, es la única variedad compacta tridimensional en la que todo lazo o círculo cerrado (1-esfera) se puede deformar (transformar) en un punto. Este último enunciado es equivalente a decir que sólo hay una variedad cerrada y simplemente conexa de dimensión 3: la esfera tridimensional.
En este enlace puedes continuar leyendo el artículo de la wikipedia
Otros enlaces sobre la conjetura de Poincaré y sobre Perelman, que fué quien la demostró en 2003:
http://fronterad.com/?q=conjetura-poincare-resuelta-por-perelman
http://www.sinewton.org/numeros/numeros/43-44/Articulo04.pdf
http://gaussianos.com/explicacion-del-teorema-de-poincare-perelman/
http://www.matematicasdigitales.com/perelman-y-la-conjetura-de-poincare/
https://eltrasterodepalacio.wordpress.com/2012/09/04/la-conjetura-de-poincare-grigori-perelman-y-su-vida-singular/
http://www.portalplanetasedna.com.ar/hombre_genio.htm
Te habrás dado cuenta de que para saber sobre la conjetura de Poincaré hay que saber de topología
http://es.wikipedia.org/wiki/Topolog%C3%ADa
http://www.ehu.eus/~mtwmastm/sigma20.pdf
http://definicion.de/topologia/
Hay otra precisión importante que hacer para comprender "de que van las matemáticas". Se trata de la diferencia entre COMPROBAR y DEMOSTRAR
Esta diferencia está muy bien ilustrada en el siguiente enlqce:
http://gaussianos.com/una-creencia-no-es-una-demostracion/
Volvamos a las conjeturas:
Naturalmente hay muchas otras conjeturas que en la actualidad siguen siendo conjeturas. Una de ellas, que además es de las que son fáciles de entender, es la conjetura de Collatz a la que está dedicada esta entrada.
El enunciado es muy sencillo:
- Si el número es par, se divide entre 2.
- Si el número es impar, se multiplica por 3 y se suma 1.
Si reptimos este proceso una y otra vez, siempre acabaremos encontrando el número 1, a partir del cual se repite la secuencia 1, 4, 2, 1 ..... indefinidamente
Para acabar de entender lo que esto quiere decir, elegimos un número entero positivo, por ejemplo el 13.
Como es impar lo multiplicamos por 3 (39) y le añadimos 1 (40)
Como 40 es par, lo dividimos entre 2, y obtenemos 20
Como 20 es par, lo dividimos entre 2 y obtenemos 10
Como 10 es par, lo dividimos entre 2 y obtenemos 5
Como 5 es impar, lo multiplicamos por 3 (15) y le sumamos 1, obteniendo 16
Como 16 es par, lo dividimos entre 2, y obtenemos 8.
Como 8 es par, lo dividimos entre 2 y obtenemos 4
Como 4 es par, lo dividimos entre 2 y obtenemos 1
¡Ya hemos llegado al 1!
A partir de aquí siempre se obtiene la secuencia 4, 2, 1, 4, 2, 1.... ....
Si partimos de 3, obtenemos la sucesión 3, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1... ....
Ahora es cuestión de armarse de lápiz, papel y calculadora y ponerse a comprobar casos concretos.
Siempre llegaremos a la fatídica secuencia 1, 4, 2, 1, 4, 2, 1..... ....
(Se han hecho cálculos por ordenador, comprobando que esto es cierto desde el 1 hasta el $ 2^{58} $ )
Pero ¿porqué siempre llegamos a esta secuencia 1 2 4 1 2 4 1 .... ?
Eso es lo que no se sabe.
Podemos informarnos en las siguientes direcciones:
http://www.unocero.com/2013/02/13/pruebe-la-conjetura-de-collatz/
http://es.wikipedia.org/wiki/Conjetura_de_Collatz
http://matesmates.wordpress.com/2013/01/16/conjetura-de-collatz/
http://gaussianos.com/posible-demostracion-de-la-conjetura-de-collatz/
http://www.xtec.cat/~bfiguera/tcollatz.pdf
Ésta es muy interesante, no entra en cálculos, aunque menciona números complejos y fractales:
http://gaussianos.com/la-representacion-fractal-de-la-conjetura-de-collatz/
http://gaussianos.com/la-representacion-fractal-de-la-conjetura-de-collatz/print/
Un vídeo sobre la conjetura de Collatz, corto, claro, divulgativo:
https://www.youtube.com/watch?v=HpcYW08Ug7g
Si has llegado hasta aquí y has leído toda la información o parte de ella y has hecho algunos cálculos, estás en condiciones de leer esta explicación y un montón de sugerencias en los comentarios:
http://gaussianos.com/la-conjetura-de-collatz/#comments
Acceso al programa para calcular los números de Collatz
http://www.enric.es/php/conjetura-collatz/?f=31
Bueno, en conclusión, asuntos abiertos en matemáticas, los hay a montones, éste es uno de ellos, facilito de entender, pero desde luego, nada fácil de demostrar.
En conexión con esto, nos podemos preguntar qué asuntos se investigan hoy día en matemáticas, es decir aún no están demostrados.
Es un tema diferente, pero relacionado con lo que se ha tratado en esta entrada: ¿en qué consisten las matemáticas que se hacen hoy, las que aún no están del todo inventadas sino que están siendo investigadas y creadas por los matemáicos de hoy día?
Pues la serie de vídeos ¿qué hace hoy un matemático? intenta contestar esa pregunta.
http://www.youtube.com/watch?v=ux0XBD2tmFY&feature=share
http://www.youtube.com/watch?v=p9MnFSDOwGA
Como ejemplo, en el año 2013 se han demostrado varias conjeturas de teoría de números, que vienen descritas en el blog gaussianos:
http://gaussianos.com/resuelta-una-conjetura-de-erdos-sobre-congruencias/
http://gaussianos.com/parece-ser-que-demostrada-la-conjetura-debil-de-goldbach/
http://gaussianos.com/posible-avance-en-el-estudio-de-los-primos-gemelos/
Por cierto que una novela que te permitirá familiarizarte con la conjetura de Goldbach, de una manera relajada y entretenida es "el tío Petros y la conjetura de Goldbach" que tienes comentado en este enlace:
http://www.librosmaravillosos.com/conjeturagoldbach/
Con todo este material puedes convencerte que la matemática es un mundo vivo, con partes ya hechas y otras en construcción, que va mucho más allá de lo que se estudia en Secundaria o en la Universidad.
Un tema parecido es el de la constante de Krapekar
Copio y pego aquí lo que dice la Wikipedia
El número 6174 es conocido como la Constante de Kaprekar en honor de su descubridor el matemático indio Dattatreya Ramachandra Kaprekar. Este número es el resultado de la aplicación repetida de la Operación de Kaprekar1 2 que consiste en los siguientes pasos:
- Escoger cualquier número de cuatro dígitos (con limitadas excepciones, véase más abajo).
- Ordenar los cuatro dígitos en orden ascendente, para obtener el minuendo de una resta.
- Ordenar los mismos cuatro dígitos en orden descendente, para obtener el sustraendo de la misma resta.
- Calcular el resto, restando el sustraendo del minuendo.
- Si el resto no es igual a 6174, repetir los cuatro pasos anteriores, añadiendo ceros a la derecha al minuendo y a la izquierda al sustraendo, siempre que sea necesario para completar los cuatro dígitos.
Por ejemplo, supongamos que partimos del número de cuatro dígitos 5342:
- 5432 – 2345 = 3087
- 8730 – 0378 = 8352
- 8532 – 2358 = 6174
- 2111 – 1112 = 0999
- 9990 – 0999 = 8991
- 9981 – 1899 = 8082
- 8820 – 0288 = 8532
- 8532 – 2358 = 6174
- A continuación, enlaces para ampliar:
- video sobre la constante de Krapekar
http://en.wikipedia.org/wiki/6174_(number)
http://plus.maths.org/content/os/issue38/features/nishiyama/index
http://www.ehu.eus/~mtpalezp/mates/agunegros.pdf?
http://gaussianos.com/la-constante-de-kaprekar/
http://www.microsiervos.com/archivo/ciencia/6174.html
http://divulgadores.com/la-constante-de-kaprekar/
http://blogs.20minutos.es/mati-una-profesora-muy-particular/tag/constante-de-kaprekar/
Para terminar, unas indicaciones para trabajar la conjetura de Collatz en Educación Secundaria, en el marco de un taller de matemáticas
https://www.blogger.com/comment.g?blogID=3219117272340648003&postID=935806891704841038&page=1&token=1457800122525
Añado un debate interesante sobre esto
http://gaussianos.com/%C2%BFquien-no-tiene-una-demostracion-de-la-conjetura-de-goldbach/#comment-743013
OTRO ENUNCIADO DE LA CONJETURA DE COLLATZ
https://alexmoqui.wordpress.com/2012/04/09/conjetura-de-collatz/
Trabajo matemático sobre la conjetura de Collatz
Otro recurso sobre la conjetura de Collatz
https://parafernaliasviendolasformulas.blogspot.com/2023/12/conjetura-de-collatz-y-constante-de.html
Me propongo profundizar en estos temas en cuanto tenga tiempo
Hasta la próxima entrada




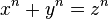






No hay comentarios:
Publicar un comentario
Tu opinión respetuosa con elementales normas de cortesía y convivencia, será siempre bienvenida